Question

Hello please help me through 11-13 .

Answer 1

Explanation:

Points to remember while solving a system of linear equations,

1). If the equations have same slope, solution of the system will have no solution.

2). If both the equations are same, system will have infinitely many solutions.

3). If both the equations have different coefficients of variables, system of equations will have exactly one solution.

Question 11,

ax + 4y = 10 ------ (1)

-9x - 6y = -15

-3x - 2y = -5

-6x - 4y = -10

6x + 4y = 10 -------(2)

For infinitely many solutions,

Coefficients of variables will be same.

a = 6 will be the answer.

Option B is the correct option.

Question 12,

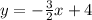`y=-(3)/(2)x+4` ---------(1)

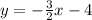`y=-(3)/(2)x-4` ----------(2)

Since, slopes of both the equations are same as
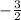`-(3)/(2)`, lines will be parallel.

System will have NO SOLUTION.

Question 13,

x + 3y = 6 ------- (1)

6x + 18y = 36

x + 3y = 6 -------- (2)

Both the equations are same.

Therefore, system of the equations will have infinitely many solutions.

2x - 3y = -3 ------(1)

4x + 6y = 18

2x + 3y = 9 -------(2)

Coefficients of the variables are different, therefore, one solution.

3x + 2y = 6 -------(1)

6x - 4y = 24

3x - 2y = 12 -------(2)

One solution.

8x - 10y = 6

4x - 5y = 3 -------(1)

-4x + 5y = 3

4x - 5y = -3 ------(2)

One solution.

4x + 10y = 16

2x + 5y = 8 --------(1)

10x + 25y = 40

2x + 5y = 8 --------(2)

Infinitely many solutions.