Question

The radius of Earth is 6.371 × 103 km.Find the altitude above Earth’s surface where Earth’s gravitational field strength would be two-thirds of its value at the surface.Find the altitude above Earth’s surface where Earth’s gravitational field strength would be one-fourth of its value at the surface.

Answer 1

Given,

The radius of the earth, r=6.371×10³ km=6.371×10⁶ m

The gravitational strength at the surface of the earth is given by,

`g=(GM)/(r^2)_{}`

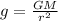
Where G is the gravitational constant and M is the mass of the earth.

Thus the gravitational field strength at a height h, where the gravitational field strength would be two-third of its values at the surface is,

`g_h=(GM)/((r+h)^2)=(2g)/(3)`

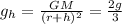
Thus,

`\begin{gathered} (GM)/((r+h)^2)=(2GM)/(3r^2) \\ \Rightarrow(3)/(2)r^2=(r+h)^2 \\ \Rightarrow\sqrt[]{(3)/(2)}r=r+h \\ \Rightarrow h=r(\sqrt[]{(3)/(2)}-1) \end{gathered}`

On substituting the value of r,

`\begin{gathered} h=6.371*10^6(\sqrt[]{(3)/(2)}-1) \\ =6.371*10^6(0.225) \\ =1.433*10^6\text{ m} \end{gathered}`

Thus the earth's gravitational field strength would be two-thirds of its value at the surface at a height of 1.433×10⁶ m above the surface.

The height at which the gravitational field strength would be one-fourth its value at the surface is given by,

`g_H=(GM)/((r+H)^2)=(g)/(4)`

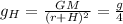
Thus,

`\begin{gathered} (GM)/((r+H)^2)=(GM)/(4r^2) \\ 4r^2=(r+H)^2 \\ \sqrt[]{4}r=r+H \\ \Rightarrow H=2r-r=r \end{gathered}`

Therefore,

`H=6.371*10^6\text{ m}`

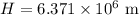
Thus the earth's gravitational field strength would be one-fourth of its value at the surface at a height of 6.371×10⁶ m above the surface.