Question

We consider f a function defined on R by f(x) = sin(√x), (x >= 0).1) Determine the first derivative of f, f'(x).2) Establish the relation 4xf'(x)² + f(x)² = 1

Answer 1

First, let's calculate the derivative:

`f^(\prime)(x)=(d)/(dx)(\sin \sqrt[]{x})`

Here we have a compounded function, so we need to apply the chain rule:

`f^(\prime)(x)=\cos \sqrt[]{x}\cdot(d)/(dx)(\sqrt[]{x})`

Finally, we obtain:

`f^(\prime)(x)=\cos \sqrt[]{x}\cdot(\frac{-1}{2\cdot\sqrt[]{x}})`
`f^(\prime)(x)=-\frac{\cos \sqrt[]{x}}{2\cdot\sqrt[]{x}}`

Now, let's establish the relationship:

`4x\cdot f^(\prime)(x)^2+f(x)^2=1`

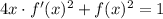
replacing the expressions of the functions:

`4x\cdot(\frac{\cos\sqrt[]{x}}{2\cdot\sqrt[]{x}})^2+\sin ^2\sqrt[]{x}=1`
`4x\cdot\frac{\cos^2\sqrt[]{x}}{2^2\cdot\sqrt[]{x}^2}+\sin ^2\sqrt[]{x}=1`
`4x\cdot\frac{\cos^2\sqrt[]{x}}{4x}+\sin ^2\sqrt[]{x}=1`

We can cancel the terms 4x in the first term of the expression:

`\cos ^2\sqrt[]{x}+\sin ^2\sqrt[]{x}=1`

From the Pythagorean identity, we know that the sum of cosine squared, plus sine squared of any angle is always equal to 1:

`\sin ^2\theta+\cos ^2\theta=1`

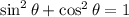
Then, we confirm that the relationship established in 2) is correct:

`\begin{gathered} \cos ^2\sqrt[]{x}+\sin ^2\sqrt[]{x}=1 \\ \\ 1=1 \end{gathered}`