y = 1/2(x) - 1
To solve this question, we would use the midpoint formula to find the x and y coordinates.
Mid point formula:
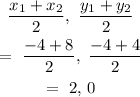
Midpoint = (2,0)
Then we would find the slope:
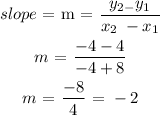
Since the slope = -2, the negative reciprocal of slopes give perpendicular.
the reciprocal = -1/-2 = 1/2
Then we apply linear quation- the slope intercept form to get the constant (c):
y = mx + c
from our midpoint (2,0), y = 0 and x =2
0 = 1/2(2) + c
c = -1
The equation for the perpendicular bisector:
y = 1/2(x) - 1