Question

-3x^2-8x+3 could someone please help me with a method that I could use to make these problems easier my memory is so bad and I've taken notes but it gets confusing. a step by step would be nice

Answer 1

We want to factor the expression:

`-3x^2-8x+3`

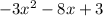
This is a trinomial of the form ax^2+bx+c. We will use a step by step method.

1. Multiplying and dividing by the leading coefficient.

We first identify which one is the leading coefficient of the trinomial, this is the one that is at the side of the x squared. In this case, it is -3.

Then we multiply all the polynomial by -3, and divide by that number.

`(-3(-3x^2-8x+3))/(-3)`

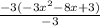
But we are NOT GOING TO MULTIPLY THE CENTER NUMBER, as shown:

`=(9x^2-8x(-3)-9)/(-3)`

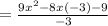
2. Factoring the leading term

We will factor the leading term, expressing it as a monomial squared. In this case, we see that 9x² equals (3x)². Thus,

`=((-3x)^2-8(-3x)-9)/(-3)`

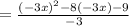
3. Factorizing as a trinomial of the form x²+bx+c.

In this case, we have to find two numbers that multiplied are -9, and that added give as result -8. We get that those numbers are -9 and +1, as:

`\begin{gathered} -9\cdot1=-9 \\ -9+1=-8 \end{gathered}`

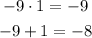
Thus, we factor the numerator as shown:

`=((-3x-9)(-3x+1))/(-3)`

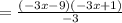
4. Dividing one or two terms over the denominator.

We search which one of the terms has all the coefficients divisible by the denominator, -3. In this case, as both -3 and -9 are divisible by 3, we get:

`=(x+3)(-3x+1)`

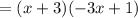
Thus, the factorization of the polynomial given is (x+3)(-3x+1).