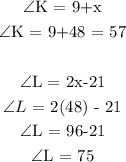Question

16. In AJKL, if m angle K is nine more than m angle j and m angle L is 21 less than twice m angle 2, find the measure of each angle. m angle 2 = m angle K = m angle L =

Answer 1

The individual angle measures of triangle JKL are;

Here, we want to find the measure of each angle in triangle JKL

Let us start this by assigning a variable to represent angle j

Let us have the variable as x

Angle k is nine more than angle j

Thus;

`\begin{gathered} \angle K\text{ = 9 + }\angle J \\ \angle K\text{ = 9+x} \end{gathered}`

Furthermore, L is 21 less than two times the measure of angle J

`\begin{gathered} \angle\text{L = 2}\angle J\text{ - 21} \\ \angle\text{L = 2x-21} \end{gathered}`

Mathematically, the sum of the angles of a triangle is 180

Thus, we have it that;

`\begin{gathered} \text{x + 2x-21 + x + 9 = 180} \\ 4x-21+9\text{ = 180} \\ 4x-12\text{ = 180} \\ 4x\text{ =180+12} \\ 4x\text{ = 192} \\ x\text{ = }(192)/(4) \\ x\text{ = 48} \end{gathered}`

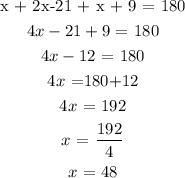
Thus, we have the measure of angke J as 48

For K and L, we simply substitute the value of x

We have;

`\begin{gathered} \angle\text{K = 9+x} \\ \angle\text{K = 9+48 = 57} \\ \\ \angle\text{L = 2x-21} \\ \angle L\text{ = 2(48) - 21} \\ \angle\text{L = 96-21} \\ \angle\text{L = 75} \end{gathered}`