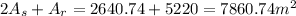Question

A training field is formed by joining a rectangle and two semicircles, as shown below. The rectangle is 90 m long and 58 m wide.Find the area of the training field. Use the value 3.14 for , and do not round your answer. Be sure to include the correct unit in your answer.

Answer 1

The area of the figure is the sum of the area of the two semi-circles and that of the rectangle.

Given a rectangle of length, l, and width, w, the area of the rectangle is given as:

`A_r=l* w`

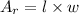
The area of a semicircle with radius r has an area that is half that of a circle.

Hence,

`A_S=(\pi r^2)/(2)_{}`

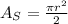
Substitute the values l=90 and w=58 into the area of a rectangle:

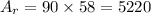
`A_r=90*58=5220`Since the semicircles are two, hence the area would be:
`2A_s=2((\pi r^2)/(2))=\pi r^2`

The radius (r) is half the length of the diameter (d):

`r=(d)/(2)`

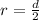
Substitute d=58 which is also the width of the rectangle:

`r=(58)/(2)=29`

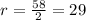
Substitute r=29 into the area of two semicircles:

`\begin{gathered} 2A_(s=)\pi r^2;r=29,\pi=3.14 \\ \Rightarrow3.14(29)^2=2640.74 \end{gathered}`

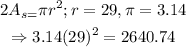
Add the areas 2As and Ar to get the area of the figure:

`2A_s+A_r=2640.74+5220=7860.74m^2`