Question

A rectangle has perimeter 86 and it’s length is 1cm more than twice it’s width.Part A: Using the definition of perimeter, write an equation for P in terms of L and W.Part B: Using the relationship given in the problem statement, write an equation for L in terms of W.what is the Length, and what is the width?

Answer 1

The length is given to be L, and width is given to be W.

The Perimeter, P of a rectangle is given as:

`P=2L+2W`

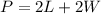
It is given that P=86, substitute this into the equation:

`86=2L+2W`

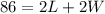
It is also given that the length is 1cm more than twice its width, it follows that:

`L=2W+1`

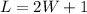
This gives the equation for L in terms of W.

Substitute this into the first equation:

`86=2(2W+1)+2W`

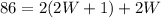
Solve the equation for W:

`\begin{gathered} 86=4W+2+2W \\ \Rightarrow86=6W+2 \\ \Rightarrow86-2=6W \\ \Rightarrow84=6W \\ \Rightarrow6W=84 \\ \Rightarrow W=(84)/(6)=14\text{ cm} \end{gathered}`

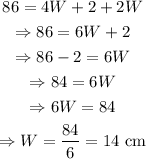
The width is 14 cm.

Substitute the value of the width into the equation for L:

`\begin{gathered} L=2W+1 \\ \Rightarrow L=2(14)+1 \\ \Rightarrow L=28+1 \\ \Rightarrow L=29\text{ cm} \end{gathered}`

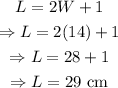
Answers:

The equation for P in terms of L and W is: P=2L+2W

The equation for L in terms of W is: L=2W+1

The length is 29 cm and the width is 14 cm.