Given three sides of a triangle, and to determine the types of triangle.
To achieve this, we will first define what an acute, right, and obtuse triangles are. Then, find each of the angles of the triangle
Step 1: Define acute, obtuse, and right-angled triangle
An acute triangle is a triangle that has all its three angles an acute angle (acute angles are angles that are less than 90 degrees)
An obtuse triangle is a triangle that has one its angles as obtuse angle (obtuse angles are angles that are greater than 90 degrees but less than 180 degrees
A right-angled triangle is a triangle that has one of its angles as a right angle ( right angles are angle 90 degrees)
Step 2: Calculate each of the angles of the given triangles
Let the given triangle be represented as triangle ABC shown above
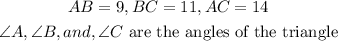
With the 3 sides given, we can get an angle using cosine rule
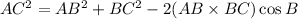
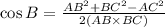
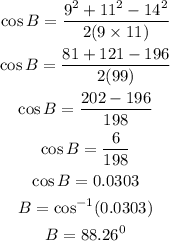
![undefined]()