Question

The first tank shows is half filled with water. The water from first tank is poured into the second tank, which is empty. What height will the water reach in the second tank?

Answer 1

We have here two prisms. In general, the volume for these two prisms is equal to the area of the base times the height of the prism.

Then, we need to obtain the total volume that the water occupies in the first tank. Then with this information, we can find the height of the water reach in the second tank.

Calculating the volume of water in the first tank

We have the following information for the whole tank:

length (l) = 9 inches

width (w) = 6 inches

height (h) = 8 inches

However, the water has a height of only half of the tank. Then, we have that the height for water is only 4 inches. Then, the volume of water is:

`V_{\text{water}}=l\cdot w\cdot h\Rightarrow V_(water)=9in\cdot6in\cdot4in\Rightarrow V_(water)=216in^3`

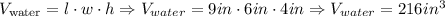
Calculating the height for water in the second tank

We have that the volume of a prism is the product of the base area times the height of the prism:

`V_{\text{prism}}=B\cdot h`

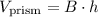
And we have already obtained the volume we need to pour in the second tank, V = 216 cubic inches. We only need to calculate the base area of the second tank as follows:

`B_(2nd)=l\cdot w`

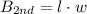
And we have that l = 8 inches, and w = 5 inches, then the base area is:

`B_(2nd)=8in\cdot5in\Rightarrow B_(2nd)=40in^2`

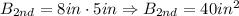
And, we finally need to do as follows to find the height that the water will have in the second tank:

• Vprism = 216 cubic inches

,

• B = 40 square inches

Thus, we have:

`V_{\text{prism}}=B\cdot h\Rightarrow216in^3=40in^2\cdot h`

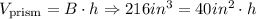
Dividing both sides of the equation by 40 square inches:

`(216in^3)/(40in^2)=(40in^2)/(40in^2)\cdot h\Rightarrow h=(216in^3)/(40in^2)\Rightarrow h=5.4in`

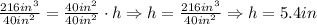
Then, the height that the water will reach in the second tank will be 5.4 inches.