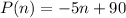Question

A clothing business finds there is a linear relationship between the number of shirts, n it can sell and the price. P. it cancharge per shirt. In particular, historical data shows that 2 thousand shirts can be sold at a price of $80 each, and that 5thousand shirts can be sold at a price of $65 each.Find the equation of the form P(n) = mn + b that gives the price P they can charge for n thousand shirts.

Answer 1

The price per shirt P and the amount of shirts(in thousands) n are related by a linear relationship, therefore, their relationship has the following format

`P(n)=mn+b`

Where m represents the slope of that line and b the y-intercept.

We know that 2 thousand shirts can be sold at a price of $80 each, and that 5

thousand shirts can be sold at a price of $65 each. Those statements tells us two points that belongs to our line, they are (2, 80) and (5, 65). To find the coefficients of our equation, we can just substitute those points in the line equation and then solve the resulting system for m and b.

Using the points in our equation, we have

`\begin{cases}80=2m+b \\ 65=5m+b\end{cases}`

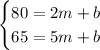
Subtracting the second equation from the first equation, we get a new equation only for m.

`\begin{gathered} 80-(65)=2m+b-(5m+b) \\ 80-65=2m+b-5m-b \\ 15=-3m \\ -3m=15 \\ m=-(15)/(3) \\ m=-5 \end{gathered}`

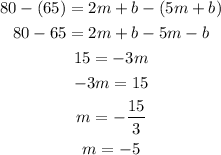
To find b, we can use this value for m in any of the equation of our system

`\begin{gathered} 80=2(-5)+b \\ 80=-10+b \\ 90=b \\ b=90 \end{gathered}`

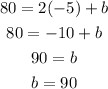
Using those values, we have the following line equation

`P(n)=-5n+90`