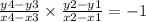Question

If A[X1.71), 8X2, y2), CX3, Yz), and Dlxq ya) form two line segments, AB and CD, which condition needs to be met to prove ABICD?ОА. У4-У2, Уз-у, -X - X, X, — х,Ов. У4 - Уа, х4 – х.=0У, —x, x, — Х.ОС.У4-УУ. -У -1X - X, X, -х,OD. У. -У, Х.-х. -1х. — Х. У4 - У.=ОЕ.ул - Уа= 0У, -х,x, – х.

Answer 1

Given:

A(x1, y1), B(x2, y2), C(x3, y3), D(x4, y4).

Where AB and CD form two line segements.

Let's determine the condition which shows that AB is perpendicular to CD.

The slope of a perpendicular line is the negative reciprocal of the slope of the other line.

To show two lines are perpdincular, apply the formula:

`m_(AB)* m_(CD)=-1`

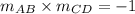
Where m is the slope.

Now, apply the slope formula:

`\begin{gathered} m_(AB)=(y2-y1)/(x2-x1) \\ \\ m_(CD)=(y4-y3)/(x4-x3) \end{gathered}`

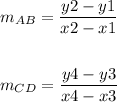
Thus, we have:

`(y4-y3)/(x4-x3)*(y2-y1)/(x2-x1)=-1`

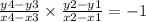
Therefore, the condition that needs to be met to prove that AB is perpendicular to CD is:

`(y4-y3)/(x4-x3)*(y2-y1)/(x2-x1)=-1`

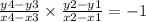
ANSWER: C

`(y4-y3)/(x4-x3)*(y2-y1)/(x2-x1)=-1`