Final Answer:
The correct value for
 is 10, and the sequence is 40, 20, 70.
is 10, and the sequence is 40, 20, 70.
Step-by-step explanation:
To find the value of
 , we need to observe the given sequence of numbers: 40, 2x, 140. The pattern involves multiplying the first number by
, we need to observe the given sequence of numbers: 40, 2x, 140. The pattern involves multiplying the first number by
 to get the second number and then multiplying the second number by 3.5 to get the third number.
to get the second number and then multiplying the second number by 3.5 to get the third number.
Let's break it down step by step:
1.
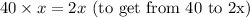
2.
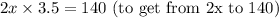
Now, we can solve for
 in the first equation:
in the first equation:
![\[40 * x = 2x\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/sx8p8n9mxj4hqfjbnltk48oouqgnxo27d7.png)
Divide both sides by 40:
![\[x = (2x)/(40)\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/3f8yietgfdcj5t749xioqn9gfm4mer1ib5.png)
Solving for
 :
:
![\[x = (1)/(20) * 2x\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/tbemfsvnz3wrbzm8jxjofhx72vi373ba6i.png)
![\[x = (1)/(10) * x\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/5x494vaibt5477qaknf3n71n92eybwlf89.png)
![\[10x = x\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/zwogsbqlggciaqkn7nlbkqkn49ai2vksax.png)
Now, we can safely say that
 must be 10. However, it's always good to check this value in the original sequence:
must be 10. However, it's always good to check this value in the original sequence:
1.
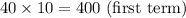
2.
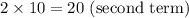
3.
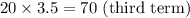
So, the correct value for
 is indeed 10, and the sequence is 40, 20, 70.
is indeed 10, and the sequence is 40, 20, 70.