Question

DJ is making a playlist for a radio show, he is trying to decide what 10 songs to play and in what order should they be played in .if he has his choices narrow down to 7blues,7 disco,5 pop and 7 reggae songs, he wants to play all five pop songs how many different playlists are possible? Express your answer in scientific notation rounding to the hundredth place

Answer 1

We have to find how many 10-song lists can the DJ play.

The condition is that all 5 pop songs are included in the list.

In this problem, the order of the songs is relevant.

We have a total of 26 songs (7 blues, 7 disco, 5 pop and 7 reggae songs).

We will start by calculating how many possible permutations we can do with these 26 songs. Of course, this will include options that are not valid, as they may not include all the pop songs.

To correct that, we will substract the options that don't include all the pop songs.

For the 26 songs in playlists of 10 songs, we can calculate the permutation as:

`P(26,10)=(26!)/((26-10)!)=(26!)/(16!)=19275223968000`

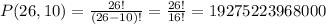
Then we have to find the playlist that do not include all the 5 pop songs. If we miss one pop song, we have an invalid playlist.

Then, we can think that we have 25 options (one pop song is missing) to arrange the 10-song playlist.

Alternative solution:

We have to find a way to identify which playlists include all five pop songs and which are not.

We have 26 options for the first song, 5 of them are pop songs, but we can either choose a pop song or not.

The same happens for the second song, where we have 25 options (all but the one we choose for the first song).

Then, applying the same concept we have 23 for the 3rd, 22 for the 4th and 21 for the 5th.

Then, at this point