Question

Juan Carlos is using successive approximation to estimate a positive solution for()=()f(x)=g(x), where()=5−2f(x)=5x−2and()=−5+2g(x)=−5x+2. The table shows the results for different input values of

Answer 1

Given:

f(x) =5x - 2

g(x) = -5x + 2

Part A:

To find the solution, when f(x)=g(x):

`\begin{gathered} 5x-2=-5x+2 \\ 10x=4 \\ x=(4)/(10) \\ x=0.4 \end{gathered}`

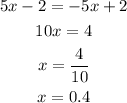
Hence, the closest possible solution, to the nearest tenth is f(x)=g(x) is 0.4.

Part B:

To find the intersection point:

From the part A, we have the solution x=0.4.

Hence, the intersection point is,

Substitute x=0.4 in any of the two function we get,

`\begin{gathered} f\mleft(0.4\mright)=5(0.4)-2 \\ =2-2 \\ =0 \\ g(0.4)=-5(0.4)+2 \\ =-2+2 \\ =0 \end{gathered}`

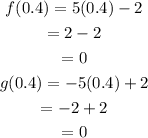
Hence, the intersection point is, (0.4,0).