Question

Describe the steps you can use to find an average of fractional amounts

Answer 1

1. first make the denominators of the set the same.
E.g.
`(2)/(7)+ (4)/(3)` =
`(6)/(21) + (28)/(21)` =
`(34)/(21)`

2. Divide the total by the number of fractions added together: In this case it was 2 so:

`(34)/(21) * (1)/(2)` =
`(34)/(42)`

3. Simplify the total:
`(17)/(21)`

Answer 2

Average of number is equal to sum of numbers by total no.

i.e.,
`Average\,=\,(Sun\,of\,numbers)/(Total\,no)`

Now when numbers/amounts are fraction then there is one extra step which is to add the fractions.

Lets say we have to find average of 2 fractions i.e.,
`(3)/(4)\,,\,(5)/(3)`

`\implies\,Average\,=\,((3)/(4)+(5)/(3))/(2)`

Step 1 : First to add the fractions find the LCM of denominator as There are unlike fractions

3 = 1 × 3

4 = 1 × 4

LCM of 3 and 4 = 3 × 4 = 12

Step 2: To make them like fraction we find equivalent fraction of each fraction whose denominator equal to 12

`(3)/(4)*(3)/(3)=(9)/(12)`

`(5)/(3)*(4)/(4)=(20)/(12)`

Step 3: Adding both fractions

`(9)/(12)+(20)/(12)=(9+20)/(12)=(29)/(12)`

Step 4: put these value in average formula

Step 5: Now we divide
`(29)/(12)` by 2 using fraction division .i.e., multiply the reciprocal of divisor with dividend

here 2 is divisor

Reciprocal =
`(1)/(2)`

`\imples Average=(29)/(12)*(1)/(2)=(29*1)/(12*2)=(29)/(24)`

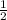
Following these steps Average of fractional amount of any no can be found.