Question

Help me!Your alarm clock has a 97.5% probability of working on any given morning. What is the probability it will NOT work tomorrow? 50%97.5%5.5%2.5%

Answer 1

The second axiom of probability states that the probability of the whole sample space S is equal to 1, or, expressed as a percentage it is equal to 100%.

For this example the Sample space is formed by two complementary events, I will call A and Ac:

A: "The alarm clock works on any given morning"

Ac: "The alarm clock does not work on any given morning"

We know that the probability of A is 97.5%. Following the second axiom, we know that the probability of the sample space is equal to the sum of the probabilities of all events that conform it, and that it is equal to 100%:

`P(S)=P(A)+P(Ac)`

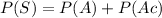
If P(S)=100% and P(A)=97.5%, then:

`\begin{gathered} 100\%=97.5\%+P(Ac) \\ P(Ac)=100\%-97.5\% \\ P(Ac)=2.5\% \end{gathered}`

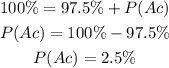
The probability that the alarm clock will not work tomorrow is 2.5%