Question

the Since the radius is an imaginary value, the equation is not a real circle, Complete the squares for each quadratic, list the center and radius, then graph each circle a) Ting its translated center: r2 =-5 r=√ 5 = i5 conic, th by the stant fa Co Paral poin ver an Exercises 12.3 Complete the following: fo 1. d) x² + 2x + y² – 4y = 4 (c) 2r2 + 2y2 + 3x - 5y = 2 e) x2 + y2 + 3x = 4 (g) x2 + y2 + 4x = 0 (i) r2 + y2 + 2mr - 2ny = 0 b) x2 + y2 - 4x = 0 x² + y² 2x - 8y = 8 4x2 + 4y2 - 16x + 24y = -27 (h) x2 + y2 – 7y = 0 (1) x2 + y2 - 2ax + 2by = c

Answer 1

EXPLANATION

Given the quadratic equation 4x^2 + 4y^2 -16x +24y=-27

As we already know, the circle equation with a radius r, centered at (a,b) is;

`(x-a)^2+(y-b)^2=r^2`

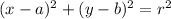
Dividing by coefficient of square terms: 4

`x^2+y^2-4x+6y=-(27)/(4)`

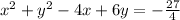
Group x-variables and y-variables together:

`(x^2-4x)+(y^2+6y)=-(27)/(4)`

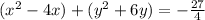
Convert x to square form:

`(x^2-4x+4)+(y^2+6y)=-(27)/(4)+4`

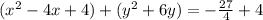
Convert to square form:

`(x-2)^2+(y+3)^2=-(27)/(4)+4+9`

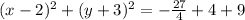
Refine -27/4+4+9

`(x-2)^2+(y-(-3))^2=((5)/(2))^2`

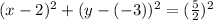
Therefore the circle properties are:

center: (a,b)=(2,-3), radius=5/2

The graph is as follows: