Question

1. Find the remainder of (3x2 + 7x + 2) / (x + 2) using the Remainder Theorem.

Answer 1

Remainder = 0

Step-by-step explanation:

The Remainder theorem says that when we divide a function f(x) by a function with the form (x - c), the remainder will be equal to f(c)

Therefore, we can rewrite the expression as:

`(3x^2+7x+2)/(x+2)=(3x^2+7x+2)/(x-(-2))_{}`

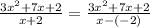
So, we can say that f(x) = 3x² + 7x + 2 and (x - c) = (x -(-2)). Then by the Remainder theorem, the remainder will be:

f(c) = f(-2)

So, f(-2) is equal to:

f(x) = 3x² + 7x + 2

f(-2) = 3(-2)² + 7(-2) + 2

f(-2) = 3(4) - 14 + 2

f(-2) = 12 - 14 + 2

f(-2) = 0

Therefore, the remainder will be 0.