Question

Audrey is buying a new car for $32,998.00. She plans to make a down payment of $4,200.00. If she's to make monthly payments of $525 for the next five years, what APR has she paid?

A. 37%
B. .37%
C. 3%
D. 3.7%

Answer 1

To solve this we are going to use the loan payment formula:
`P= ( (r)/(n)(PV))/(1-(1+ (r)/(n))^(-nt) )`

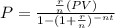
where

`P` is the amount of the regular payment

`PV` is the present debt

`r` is APR in decimal form

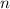`n` is the number of payments per year

`t` is the time in years

We know from our problem that Audrey is making a down payment of $4,200.00; since the cost of the car is $32,998.00, the present deb will be the cost of the car minus the down payment, so
`PV=32998-4200=28798`. We also know that she is going to make monthly payments of $525 for the next five years, so
`n=12` and
`t=12`. Let's replace the values in our formula:

`P= ( (r)/(n)(PV))/(1-(1+ (r)/(n))^(-nt) )`

`525= ( (r)/(12)(28798))/(1-(1+ (r)/(12))^(-(12)(5)) )`

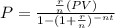
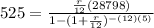
We have two ways of finding the APR: we can solve for
`r` in our equation, which is extremely difficult, or we can evaluate the given APRs and check for which one both sides of the equation are almost the same. Since the second is way easier, we are going to use it.

A. 37%

The APR should be in decimal form, so we need to convert it first; to do it we are going to divide the APR by 100%

`r=(37)/(100) =0.37`

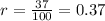
Let's replace the ARP in decimal form in our equation

`525= ( (0.37)/(12)(28798))/(1-(1+ (0.37)/(12))^(-(12)(5)) )`

`525=1059.20`

`529\\eq 1059.20`

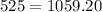
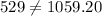
Since 529 is not equal to 1059.20, 37% is not the APR of the loan.

B. .37%

- Convert the APR to decimal form

`r=(0.37)/(100) =0.0037`

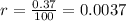
- Replace the APR

`525= ( (0.0037)/(12)(28798))/(1-(1+ (0.0037)/(12))^(-(12)(5)) )`

`525=484.49`

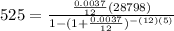
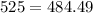
Since 525 is not equal to 484.59, .37% is not the APR of the loan.

C. 3%

- Convert the APR to decimal form

`r=(3)/(100) =0.03`

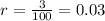
- Replace the APR

`525= ( (0.03)/(12)(28798))/(1-(1+ (0.03)/(12))^(-(12)(5)) )`

`525=517.46`

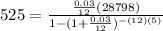
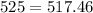
Since 525 is not equal to 517.46, 3% is not the APR of the loan.

D. 3.7%

- Convert the APR to decimal form

`r=(3.7)/(100) =0.037`

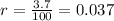
- Replace the APR

`525= ( (0.037)/(12)(28798))/(1-(1+ (0.037)/(12))^(-(12)(5)) )`

`525=526.47`

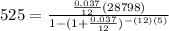
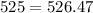
Since 525 is almost equal to 526.47, 3.7% is the APR of the loan.

We can conclude that the correct answer is D. 3.7%

Answer 2

This question is an annuity problem with cost of the car = $32,998, the present value of the annuity (PV) is given by the difference between the cost of the car and the down payment = $32,998 - $4,200 = $28,798. The monthly payments (P) = $525 and the number of number of years (n) = 5 years and the number of payments in a year (t) is 12 payments (i.e. monthly) The formula for the present value of an annuity is given by PV = (1 - (1 + r/t)^-nt) / (r/t) 28798 = 525(1 - (1 + r/12)^-(5 x 12)) / (r/12) 28798r / 12 = 525(1 - (1 + r/12)^-60) 28798r / (12 x 525) = 1 - (1 + r/12)^-60 2057r / 450 = 1 - (1 + r/12)^-60 Substituting option A (r = 37% = 0.37) 2057r / 450 = 2057(0.37) / 450 = 761.09 / 450 = 1.691 1 - (1 + r/12)^60 = 1 - (1 + 0.37/12)^-60 = 1 - 0.1617 = 0.8383 Therefore, r is not 37% Substituting option D (r = 3.7% = 0.037) 2057r / 450 = 2057(0.037) / 450 = 76.109 / 450 = 0.1691 1 - (1 + r/12)^60 = 1 - (1 + 0.037/12)^-60 = 1 - 0.8313 = 0.1687 Therefore, r is approximately 3.7%