Step-by-step explanation
We are told to compare the perimeters of the two figures given, and then determine the greater one,
To do so, we will have to split the trapezoid into two: A rectangle and A triangle as shown in the image below
Figure A is a triangle
Figure B is a rectangle
To get the perimeter, we will add the exteriors of all the sides
So we can compute the perimeter as follows
Figure A
We need to obtain x using the Pythagoras theorem
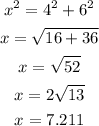
Therefore, the perimeter of the triangle is
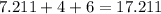
The area of the triangle is
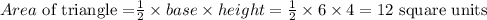
Then for figure B which is a rectangle
The perimeter of the rectangle is
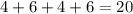
Therefore, the perimeter of the triangle is 20 units
The area of the rectangle is
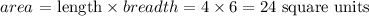
Since 20 is greater than 17.211, we can conclude that
The perimeter of the rectangle is greater than the triangle
Also comparing the area, since 24 square units are greater than 12 square units, the area of the rectangle is greater than the triangle.
so in both cases, the perimeter and area of the rectangle are greater than the triangle