Given
He has 34 coins worth $6.10
Let the number of quarters he has be x and the number of dimes hes has be y
He has 34 coins implying:
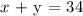
From conversion rates, we have
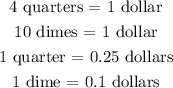
Hence, we can write:
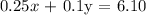
To find x and y, we have to solve the equations simultaneously
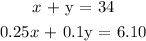
From the first equation:
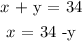
Substituting into the second equation and solving for y:

Substituting to find x:

We can conclude that Shana has 18 quarters and 16 dimes