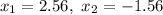Question

1. Find the solution to the system of equations. Round to the nearest tenth if necessary.f(x)=x²-5g(x) = x - 1

Answer 1

GIVEN;

We are given the following system of equations;

`\begin{gathered} f(x)=x^2-5 \\ \\ g(x)=x-1 \end{gathered}`

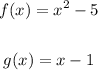
Required;

To find the solution to this system of equations.

Step-by-step solution;

For a system of equations like the one given here, the solution is the set of input values for which both equations are satisfied.

To do this, we simply equate f(x) and g(x). This is shown below;

`\begin{gathered} f(x)-g(x); \\ \\ x^2-5=x-1 \\ \\ Collect\text{ }all\text{ }like\text{ }terms; \\ \\ x^2-x=5-1 \\ \\ x^2-x=4 \\ \\ Subtract\text{ }4\text{ }from\text{ }both\text{ }sides: \\ \\ x^2-x-4=0 \end{gathered}`

We can now solve the quadratic equation that results from this as follows;

`\begin{gathered} x^2-x-4=0 \\ \\ Apply\text{ }the\text{ }quadratic\text{ }formula; \\ \\ x=(-b\pm√(b^2-4ac))/(2a) \\ \\ Where;\text{ }a=1,b=-1,c=-4 \end{gathered}`

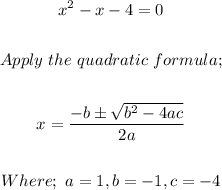
We now have;

`\begin{gathered} x=(-(-1)\pm√((-1)^2-4(1)(-4)))/(2(1)) \\ \\ x=(1\pm√(1+16))/(2) \\ \\ x=(1\pm√(17))/(2) \\ \\ x=(1\pm4.1231)/(2) \end{gathered}`

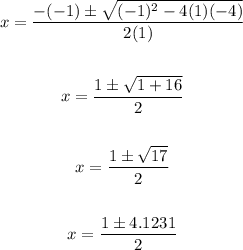
Now we can solve separately as shown below;

`\begin{gathered} x_1=(1+4.1231)/(2),x_2=(1-4.1231)/(2) \\ \\ x_1=2.56155,\text{ }x_2=-1.56155 \end{gathered}`

Rounded to the nearest tenth we now have the answer as follows;

ANSWER:

`x_1=2.56,\text{ }x_2=-1.56`