The surface area refers to the area of all the faces of the prism.
Notice that there are two equal triangular faces and three different rectangular faces.
Triangular areas.
The triangular areas would be defined by
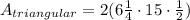
Since the area of each triangle is the semi-product between the base and the height of the triangle.
We have to transform the mixed number into a fraction.
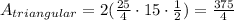
Rectangular areas.
Let's find each different rectangular area.
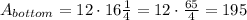
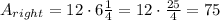
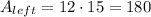
At last, we sum all the areas to find the total surface area.
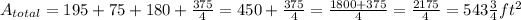
Therefore, the total surface area, in a mixed number, is 543 3/4 square feet.