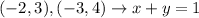The form of the linear equation is

m is the slope
b is the y-intercept
For the 1st equation on the left
m = 1
b = -3
Substitute them in the form above
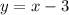
Add 3 to both sides
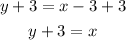
Subtract y from both sides
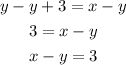
This is the 4th equation on the right side
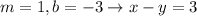
For the 2nd equation on the left
m = 1 and the line passes through the point (-1, 2)
Substitute m by 1 in the form
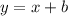
To find b substitute x by -1 and y by 2

Add 1 to each side

Substitute it in the equation

Subtract 3 from each side
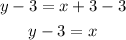
Subtract y from each side
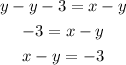
This is the 3rd equation on the right side
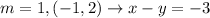
For the 3rd equation on the left
The line passes through points (-2, 3), (-3, 4)
We will use the rule of the slope to find m
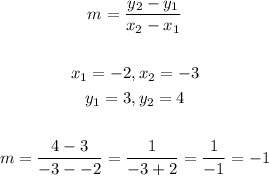
Substitute it in the form of the equation
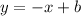
To find b use one of the two given points
I will use the first point (-2, 3)
Substitute x by -2 and y by 3 in the equation to find b
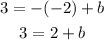
Subtract 2 from both sides
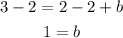
Substitute it in the equation
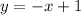
Add x to both sides
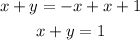
This is the 1st equation on the right side