Question

A multiple-choice exam has five possible answers for each question. For each correct answer, you are awarded 6 points. For each incorrect answer, 1 point is subtracted from your score. For answers left blank, no points are added or subtracted.a) If you do not know the correct answer to a particular question, is it to your advantage to guess? Explain.b) If you do not know the correct answer but can eliminate one possible choice, is it to your advantage to guess? Explain.

Answer 1

• (a)Yes, the expected value is 0.4, greater than 0.

,

• (b)Yes, the expected value is 0.75, greater than 0.

Explanation:

• Let the event that the student chose the correct answer = A

,

• Let the event that the student chose the wrong answer = A'

Part A

There are 5 possible answers for each question.

`\begin{gathered} P(A)=(1)/(5)=0.2 \\ P(A^(\prime))=(4)/(5)=0.8 \end{gathered}`

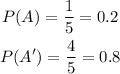
• For each correct answer, you are awarded 6 points.

,

• For each incorrect answer, 1 point is subtracted from your score.

We find the expected value:

`\begin{gathered} EV=(0.2*6)+(0.8*-1) \\ =1.2-0.8 \\ =0.4 \end{gathered}`

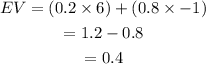
The expected value is 0.4 for any of the options chosen. Since the expected value is positive, if you do not know the correct answer to a particular question, it is to your advantage to guess

Part B

If one of the choices is eliminated, then:

`\begin{gathered} P(A)=(1)/(4) \\ P(A^(\prime))=(3)/(4) \end{gathered}`

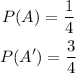
• For each correct answer, you are awarded 6 points.

,

• For each incorrect answer, 1 point is subtracted from your score.

We find the expected value:

`\begin{gathered} EV=(0.25*6)+(0.75*-1) \\ =1.5-0.75 \\ =0.75 \end{gathered}`

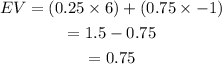
The expected value is 0.75 for any of the options chosen. Since the expected value is positive, if you do not know the correct answer but can eliminate one possible choice, it is to your advantage to guess.