Question

Solve the system by back substitution.4x + 8y + 2z +6w = 4- 2y - 12z - 4w = - 16- 2z - 2w = - 4- W= - 3----The solution set is ?? (Type an integer or a simplified fraction)

Answer 1

To answer this question, we need to start by substituting each of the values for the unknown values of each variable. However, we need to solve the easiest equation of the system.

We have that the first value we have is:

`-w=-3\Rightarrow w=3`

We can substitute this value in the previous equation to find z, as follows:

`-2z-2(3)=-4\Rightarrow-2z-6=-4`
`-2z=-4+6\Rightarrow-2z=2\Rightarrow z=(2)/(-2)\Rightarrow z=-1`

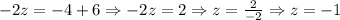
Now, we have that w = 3, and z = -1. We need to substitute these two values in the previous equation to find the value of y as follows:

`-2y-12z-4w=-16\Rightarrow-2y-12(-1)-4(3)=-16`

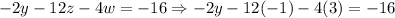
Then

`-2y+12-12=-16\Rightarrow-2y=-16\Rightarrow y=-(16)/(-2)\Rightarrow y=8`

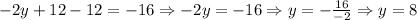
Now, we have found that the value for y = 8. We can use this value to find x as follows:

`4x+8y+2z+6w=4\Rightarrow4x+8(8)+2(-1)+6(3)=4`
`4x+64-2+18=4\Rightarrow4x+80=4\Rightarrow4x=4-80`
`4x=-76\Rightarrow x=-(76)/(4)\Rightarrow x=-19`

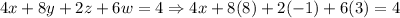
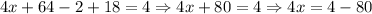
Therefore, we have found the solution set for the system. We can write it as follows:

w = 3, z = -1, y = 8, x = -19

`\mleft\lbrace(3,-1,8,-19)\mright\rbrace`

In summary, the solution set is {(3, -1, 8, -19)}.

We can check this solution set if we substitute each of these values into the given equations as follows (w = 3, z = -1, y = 8, x = -19)

`4x+8y+2z+6w=4`
`4(-19)+8(8)+2(-1)+6(3)=4\Rightarrow4=4`
`-2y-12z-4w=-16\Rightarrow-2(8)-12(-1)-4(3)=-16\Rightarrow-16=-16`
`-2z-2w=-4\Rightarrow-2(-1)-2(3)=-4\Rightarrow2-6=-4\Rightarrow-4=-4`
`-3=-3`

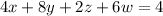
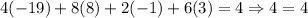
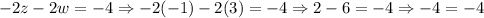
We have checked that the solution set is correct.