Question

A study is done on the population of a certain fish species in a lake. Suppose that the population size P(t) after t years is given by the following exponentialfunction.P(t) = 510 * (0.91) ^ tFind the initial population size.? Does the function represent growth or decay?O growth O decayBy what percent does the population size change each year?%

Answer 1

Given the function:

`P(t)=510*0.91^t`

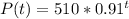
To solve this question, follow the steps below.

Step 01: Find the initial population size.

The initial population size is the population size when t = 0.

Then, substitute x by 0 to find P(0).

`\begin{gathered} P(0)=510*0.91^0 \\ P(0)=510*1 \\ P(0)=510 \end{gathered}`

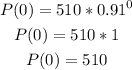
The initial population size is 510 fish.

Step 02: Find it the population size is increasing or decreasing.

To do it, find P(1) and P(2):

`\begin{gathered} P(1)=510*0.91^1 \\ P(1)=510*0.91 \\ P(1)=464.1 \end{gathered}`
`\begin{gathered} P(2)=510*0.91^2 \\ P(2)=510*0.828 \\ P(2)=422.3 \end{gathered}`

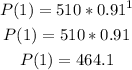
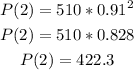
So, P(0) < P(1) < P(2). The population is decreasing.

The function represents a decay.

Step 03: Find the population change per year.

To find the population change, use the formula below:

`C(\%)=(P(t+1)-P(t))/(P(t))*100`

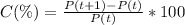
So, comparing P(0) and (P1):

`\begin{gathered} C=(464.1-510)/(510)*100 \\ C=-0.09*100 \\ C=-9\% \end{gathered}`

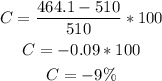
The population decreases by a percent of 9%.

In summary:

- The initial population size is 510 fish.

- The function represents a decay.

- The population decreases by a percent of 9%.