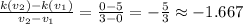Question

Using the graph of k above, find the average rate of change of k over the interval [0,3]

Answer 1

Let's start by the formula of the average rate of change. This is the same as before:

`(k(v_2)-k(v_1))/(v_2-v_1)`

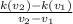
The values of v_1 and v_2 also are the same, which is the endpoints of the given interval. So

`\begin{gathered} v_1=0 \\ v_2=3 \end{gathered}`

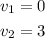
To find

`\begin{gathered} k(0) \\ k(3) \end{gathered}`

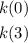
We can check the y-value that corresponds to the x-value in the graph.

We can see in the graph that for v = 0 (which is the x-value) we have k(v) = 5 (which is the corresponding y-value).

Similarly, for v = 3 we have k(v) = 0.

See here:

Now we just have to input into the formula:

`\frac{k(v_2)-k(_{}v_1)}{v_2-v_1}=(0-5)/(3-0)=-(5)/(3)\approx-1.667`