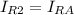Question

2) Given circuit...V1= 12VR4= 5.00R7= 3.00R2= 4.00R5= 7.00R3= 5.00R6= 3.00R2a) Find the equivalent resistance of the circuit1V1R3b) Find the current through R2R4R5c) Find the current through R3R6d) Find the power used by R4wR7e) Find the power used by R5f) Find the voltage across R6g) Find the voltage across R7

Answer 1

ANSWERS

a) R = 5.404 Ω

b) IR2 = 1.068 A

c) IR3 = 0.667 A

d) PR4 = 5.703 W

e) PR5 = 1.647 W

f) VR6 = 2 V

g) VR7 = 6.663 V

Step-by-step explanation

a) To find the equivalent resistance of the circuit we have to see which ones are connected in parallel and which ones are in series.

First we have R2 and R5 in series, so we can find en equivalent resistance that we'll call RA. Also R3 and R6 are series, so that equivalent we'll call RB:

Series resistances have to be added:

`R_A=R_2+R_5=4+7=11\Omega`
`R_B=R_3+R_6=5+3=8\Omega`

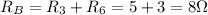
Then, resistances RB, R4 and RA are parallel. The equivalence we'll call Rc, as shown in the circuit on the right:

`R_c=(1)/((1)/(R_B)+(1)/(R_4)+(1)/(R_A))=(1)/((1)/(8)+(1)/(5)+(1)/(11))\approx2.404\Omega`

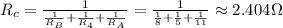
Finally R7 and RC are series, so the equivalent resistance of the circuit is:

`R_(eq)=R_C+R_7=2.404+3=5.404\Omega`

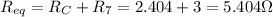
For the following points I'll do them together and separate the information requested in each point.

Voltage across R7 is requested. We can find it with the equivalent circuit B, but first we have to know the total current through the circuit. This is the total equivalent circuit:

The total current is:

`I=(V)/(R_(eq))=(12)/(5.404)\approx2.221A`

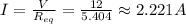
We can see in circuit B that Rc and R7 are in series so the current through them is the same. Also, this current is the total current I of the circuit. Therefore we can find the voltage across R7:

`V_(R7)=I* R_7=2.221*3=6.663V`

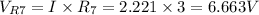
We can also use this to find the voltage across RC, which will help us find the currents in each resistance:

`V_(RC)=I* R_C=2.221*2.404\approx5.339V`

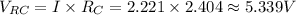
Now, since RB, R4 and RA are connected in parallel, the voltage across all of them is the same - which is VRC. With this information we can find the currents trough each of these three resistances:

`I_(R4)=(V_(RC))/(R_4)=(5.339)/(5)=1.068A`
`I_(RA)=(V_(RC))/(R_A)=(5.339)/(11)=0.485A`
`I_(RB)=(V_(RC))/(R_B)=(5.339)/(8)=0.667A`

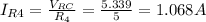
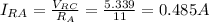
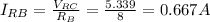
Item d asks for the power in resistence R4 and item e the power used by R5, so now that we have the current in both of them we can find the power they use. Note that the current through R5 is the same as the current through RA, because RA is the equivalente of R5 and R2 in series:

`P_(R5)=I^2_(RA)* R_5=0.485^2*7\approx1.647W`

Power used by R4 is:

`P_(R4)=I^2_(R4)* R_4=1.068^2*5=5.703W`

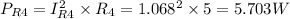
We have the current through RB, which is the same as the current through R3 (item c) and R6 so we can find the voltage across R6 (item f):

`V_(R6)=I_(RB)* R_6=0.667*3=2V`

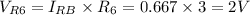
We also have the current through R2 (item b) because is the same as the current through RA:

`I_(R2)=I_(RA)`