Question

Use trigonometric identities, algebraic methods, and inverse trigonometric functions, as necessary, to solve the following trigonometric equation on the interval [0, 29).Round your answer to four decimal places, if necessary. If there is no solution, indicate "No Solution."3csc?(x) - 6 = - Scot(x)

Answer 1

x = 1.249, 2.82, 4.391, 5.961

Step-by-step explanation:

The given equation is

3csc²(x) - 6 = -8cot(x)

First, we will use the trigonometric identity

csc²(x) = 1 + cot²(x)

So, replacing csc²(x), we get:

3(1 + cot²(x)) - 6 = -8cot(x)

3(1) + 3cot²(x) - 6 = -8cot(x)

3 + 3cot²(x) - 6 = -8cot(x)

3cot²(x) - 3 = -8cot(x)

Then, add 8cot(x) to both sides, so

3cot²(x) - 3 + 8cot(x) = -8cot(x) + 8cot(x)

3cot²(x) + 8cot(x) - 3 = 0

Now, we can make a sustitution of a = cot(x), so the equation is

3a² + 8a - 3 = 0

(3a - 1)(a + 3) = 0

Solving for a, we get:

3a - 1 = 0

3a = 1

a = 1/3

or

a + 3 = 0

a = -3

Therefore, we need to find the solutions of the equations

cot(x) = 1/3

and

cot(x) = -3

Using the inverse trigonometric functions, we get:

`\begin{gathered} x=\cot ^(-1)((1)/(3))=1.249 \\ x=\cot ^(-1)(-3)=2.82 \end{gathered}`

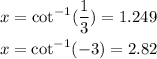
Adding π = 3.14 radians to each answer, we also get

1.249 + 3.14 = 4.391

2.82 + 3.14 = 5.961

Therefore, the answers are

x = 1.249, 2.82, 4.391, 5.961