Question

(a) Use the empirical rule to estimate the number of farms whose land and building values per acre are between $1300 and $1700.

Answer 1

The empirical rule predicts that 68% of observations falls within the first standard deviation (µ ± σ), 95% within the first two standard deviations (µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ).

The question provides the following information about the distribution:

`\begin{gathered} mean=\mu=1500 \\ standard\text{ }deviation=\sigma=200 \end{gathered}`

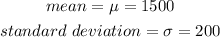
The number of farms with a value between $1300 and $1700 can be gotten using the empirical rule. Using the mean and standard deviation from the question, it is given that:

`\begin{gathered} 1500+200n=1700 \\ or \\ 1500-200n=1300 \end{gathered}`

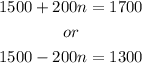
Therefore, the value of n can be calculated as follows:

`\begin{gathered} 1500+200n=1700 \\ 200n=1700-1500=200 \\ \therefore \\ n=1 \end{gathered}`

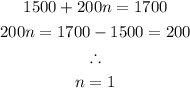
By the empirical rule, it can be said that 68% of the farms are within $1300 and $1700.

If there are 79 farms in the sample, 68% can be calculated as follows:

`\Rightarrow(68)/(100)*79=53.72`

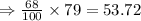
Approximately, there are 54 farms with values between $1300 and $1700.