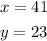Question

The sum of two numbers is 64. The difference of the two numbers is 18. What are the two numbers? Let x be the larger number and y be the smaller number.Write an equation that expresses the information in the sentence "The sum of two numbers is 64.__________________Write an equation that expresses the information in the sentence "The difference of the two numbers is 18."___________-The larger number, x is _____________.The smaller number, y is ______________

Answer 1

- The larger number is x and the smaller number is y

Sentence 1:

- "The sum of two numbers is 64"

- This means that when we add x and y, we get 64. Mathematically, this is represented as:

`x+y=64\text{ (Equation 1)}`

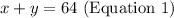
Sentence 2:

- "The difference of the two numbers is 18"

- Since x is the larger number, it means that when we subtract y from x we get 18. Mathematically, we have:

`x-y=18\text{ (Equation 2)}`

- Now that we have two equations relating x and y, we can solve them simultaneously and find the values of x and y.

- We shall apply the elimination method to solve. We would be subtracting both equations to find the value of y and after we get the value of y, we can then substitute this value of y into any of the equations, 1 or 2 to find the value of x.

- Let us perform these operations below:

`\begin{gathered} x+y=64\text{ (Equation 1)} \\ x-y=18\text{ (Equation 2)} \\ \\ \text{ Subtract both equations} \\ \\ x+y-(x-y)=64-18 \\ x+y-x+y=46 \\ 2y=46 \\ \text{Divide both sides by 2} \\ y=(46)/(2) \\ \\ y=23 \\ \\ \text{Substituting the value of }y\text{ into equation 2} \\ x-y=18 \\ x-23=18 \\ \text{Add 23 to both sides} \\ x=23+18 \\ \therefore x=41 \end{gathered}`

Final Answer

The answers to the question are:

`\begin{gathered} x=41 \\ y=23 \end{gathered}`