The formula for the z-score is as follows:
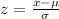
where z is the score, μ is the mean, and σ is the standard deviation.
To obtain the z-score, which indicates that the score is above the 95% of the sample, check the z-score table and look for 0.9500.
Since 0.95 is in between 0.9495 and 0.9505, the z-score must be 1.645.
Thus, we have the following:

![undefined]()