Question

Polynomial of lowest degree with real coefficients and zeros 4i and 2 - i.

Answer 1

recall that a polynomial can be written as the multiplication of multiple factors, namely of the form

`(x\text{ - c)}`

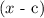
where c is a zero of the function. Note that when having a complex zero, we must have the complex conjugate as another zero. Recall that given a complex number of the form a+bi, the complex conjugate is a-bi. Recall that

`(x+a)\cdot(x-a)=x^2-a^2`

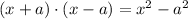
So will calculate the product of each pair of zeros:

`(x\text{ - 4i)}\cdot(x\text{ - (-4i)=(x-4i)}\cdot(x+4i)=x^2-(4i)^2=x^2-(4)^2(i)^2=x^2\text{ -16}\cdot(-1)=x^2+16`

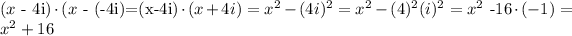
in the same manner, we would have

`(x\text{ -(2-i))}\cdot(x\text{ -(2+i))=((x -2)+i)}\cdot((x-2)-i)=((x-2)^2-i^2)=((x-2)^2\text{ +1)}`

so we have that our polynomial would be

`(x\text{ -4i)}\cdot(x+4i)\cdot(x\text{ -(2+i))}\cdot(x-(2-i))=(x^2+16)\cdot((x-2)^2+1))`

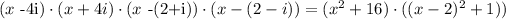
Now we only need to calculate the product of the right. So we have

`(x^2+16)\cdot((x-2)^2+1)=(x^2+16)\cdot(x^2-4x+4+1)=(x^2+16)\cdot(x^2\text{ -4x +5)}`

now we distribute to get

`(x^2+16)\cdot(x^2-4x+5)=x^2\cdot x^2\text{ -4x}\cdot x^2+5x^2+16x^2\text{ -16}\cdot4x+16\cdot5=x^4-4x^3+21x^2\text{ -64x}+80`

which would be our final answer