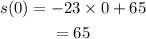Question

Questions attached as screenshot below:Please help me I need good explanations before final testI pay attention

Answer 1

The acceleration of the particle is given by the formula mentioned below:

`a=(d^2s)/(dt^2)`

Differentiate the position vector with respect to t.

`\begin{gathered} (ds(t))/(dt)=(d)/(dt)\sqrt[]{\mleft(t^3+1\mright)} \\ =-(1)/(2)(t^3+1)^{-(1)/(2)}*3t^2 \\ =(3)/(2)(t^2)/(√((t^3+1))) \end{gathered}`

Differentiate both sides of the obtained equation with respect to t.

`\begin{gathered} (d^2s(t))/(dx^2)=(3)/(2)(\frac{2t}{\sqrt[]{(t^3+1)}}+t^2(-(3)/(2))*\frac{1}{(t^3+1)^{(3)/(2)}}) \\ =\frac{3t}{\sqrt[]{(t^3+1)}}-(9)/(4)\frac{t^2}{(t^3+1)^{(3)/(2)}} \end{gathered}`

Substitute t=2 in the above equation to obtain the acceleration of the particle at 2 seconds.

`\begin{gathered} a(t=1)=\frac{3}{\sqrt[]{2}}-\frac{9}{4*2^{(3)/(2)}} \\ =1.32ft/sec^2 \end{gathered}`

The initial position is obtained at t=0. Substitute t=0 in the given position function.

`\begin{gathered} s(0)=-23*0+65 \\ =65 \end{gathered}`