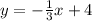Question

Determine the equation in slope-intercept form that defines line AB

Answer 1

`y=-(1)/(3)x+4`

From the graph, we can see that line AB passes through the points (-3, 5) and (3,3)

We know that the slope-intercept form of the equation of the lines goes by:

`y=mx+b`

Where:

m = slope

b = y-intercept

To get the slope, we are going to use the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Again, with the points (-3, 5) and (3, 3), we will substitute the corresponding values to the formula

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(3-5)/(3-(-3)) \\ m=(-2)/(6) \\ m=-(1)/(3) \end{gathered}`

Now, we got a slope of -1/3. Next, we need to find the y-intercept (b). We are going to solve it by using the formula y = mx + b, while substituting the point (-3, 5) and the slope -1/3.

`\begin{gathered} y=mx+b \\ 5=-(1)/(3)(-3)+b \\ 5=1+b \\ b=5-1 \\ b=4 \end{gathered}`

We now have the value of our y-intercept. Since we now have both slope (m) and y-intercept (b), we will substitute both values to the slope-intercept form of the equation of the line to get the final answer.

`\begin{gathered} y=mx+b \\ y=-(1)/(3)x+4 \end{gathered}`

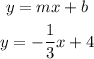
Therefore, the final answer is:

`y=-(1)/(3)x+4`