Question

Create the equation of the cubic, in standard form, that has x-intercepts of -4,-1, and 3 and passes through the point (1, 40). Verify your answer by sketching the cubic's graph on the axes below.

Answer 1

`y=-2x^3-4x^2+22x+24`

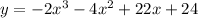
Step-by-step explanation:

The standard form of a cubic equation is given as:

`y=ax^3+bx^2+cx+d`

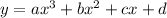
If the equation has x-intercepts of -4,-1, and 3, then we have:

At x=-4

`\begin{gathered} At\text{ x=-4} \\ 0=a(-4)^3+b(-4)^2+c(-4)+d \\ -64a+16b-4c+d=0 \end{gathered}`

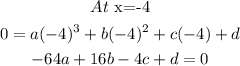
At x=-1

`\begin{gathered} 0=a\mleft(-1\mright)^3+b\mleft(-1\mright)^2+c\mleft(-1\mright)+d \\ -a+b-c+d=0 \end{gathered}`

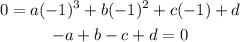
At x=3

`\begin{gathered} 0=a\mleft(3\mright)^3+b\mleft(3\mright)^2+c\mleft(3\mright)+d \\ 27a+9b+3c+d=0 \end{gathered}`

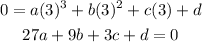
At the point (1,40)

`\begin{gathered} 40=a\mleft(1\mright)^3+b\mleft(1\mright)^2+c\mleft(1\mright)+d \\ a+b+c+d=40 \end{gathered}`

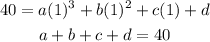
This gives us a system of equations with 4 unknowns.

`\begin{gathered} -64a+16b-4c+d=0 \\ -a+b-c+d=0 \\ 27a+9b+3c+d=0 \\ a+b+c+d=40 \end{gathered}`

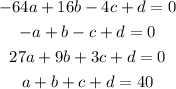
If we solve this using a calculator, we have that:

`a=-2,b=-4,c=22,d=24`

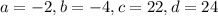
Therefore, the cubic equation will be:

`y=-2x^3-4x^2+22x+24`

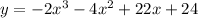
The graph of the equation is attached below:

We can clearly see the 4 given points on the graph above.