The question can be solved using an arithmetic sequence model.
The general formula for an arithmetic sequence is given to be:
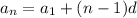
where

We can get the common difference by applying the information given into the formula.
GIVEN:
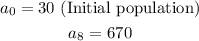
We can model the formula for the 8th term such that:
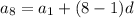
We have the value for the first term to be:

Substituting the values given, we have:
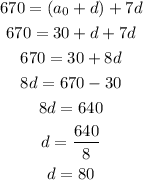
QUESTION A:
The general recursive formula is given to be:
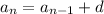
Therefore, for this sequence, the recursive formula is:
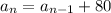
QUESTION B:
The general explicit formula for an arithmetic sequence is given to be:
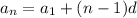
Therefore, for this sequence, the explicit formula is given to be:

QUESTION C:
In week 62, we will take n = 62:
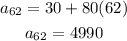
There will be 4990 beetles in week 62.
QUESTION D:
In this problem, we will make the following substitution:
Therefore, we can substitute into the explicit formula and solve for n as shown:
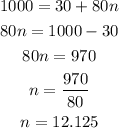
Therefore, in the 13th week, since we can't use a decimal for the weeks, the beetle population will reach 1000 beetles.