Question

What is the base 8 representation of the number 600? A) 1130 (8) B) 1310 (8) C) 1301 (8) D) 1300 (8)

Answer 1

`\begin{gathered} 1(8^{3^{}})+1(8^2)+3(8^1)+0(8^0) \\ =512+64+24+0 \\ =600 \\ \\ 1(8^{3^{}})+1(8^2)+3(8^1)+0(8^0)\text{ } \\ 1130\text{ } \end{gathered}`

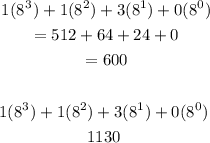
Here, we express 600 in terms of the base 8. We have to think of addends that has a root of 8 (or has a factor of 8) . To make it easier, start with 8, 8^2 and 8^3. That is 8, 64, and 512 respectively. The sum of this 3 numbers is 584. The idea is to complete the sum and make it 600. Thus there is a deficit of 16. We know that 16 has a factor of 8 and 2. So instead of having 8, we make it 3 x 8 (to include the deficit that is 16). Now we have, 3x8, 64 and 512. And the total is 600. The next step is to arrange it in decreasing order in terms of the base 8. So we have to start with 8^3, 8^2 and so on. Here we will include 8^0 (which is equal to 1) to complete the series of base 8. And since the total is already 600, we dont want to add 1 to it, so we have to multiply 8^0 by 0 . This way we can keep the sum to 600. We have 512, 64, 3X8, and 8^0x 0 (or 512,64,24 and 0) Rewriting it in terms of base 8, we have

`1(8^{3^{}})+1(8^2)+3(8^1)+0(8^0)\text{ }`

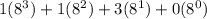
As you can see the factors are 1130 (8)

Answer:

A) 1130