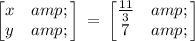Question

Solve the following system of equations using an inverse matrix. You must alsoindicate the inverse matrix, A-1, that was used to solve the system. You mayoptionally write the inverse matrix with a scalar coefficient.-6x+2y =-83x-2y = -3

Answer 1

`x\text{ = }(11)/(3),\text{ y = 7}`

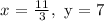
Step-by-step explanation:

Here, we want to solve the given simultaneous equation by matrix notation

Mathematically, we have it that:

`\begin{bmatrix}{-6} & {2} \\ {3} & {-2}\end{bmatrix}\begin{bmatrix}{x} & {} \\ {y} & {}\end{bmatrix}\text{ = }\begin{bmatrix}{-8} & {} \\ {-3} & {}\end{bmatrix}`

`\begin{gathered} if\text{ matrix A = }\begin{bmatrix}{a} & {b} & {} & {} \\ {c} & {d} & {} & {} \\ {} & {} & {} & {} \\ {} & {} & {} & {}\end{bmatrix} \\ \\ Then\text{ A}^(-1)\text{ = }(1)/(ad-bc)\begin{bmatrix}{d} & {-b} \\ {-c} & {a}\end{bmatrix} \end{gathered}`

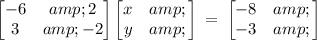
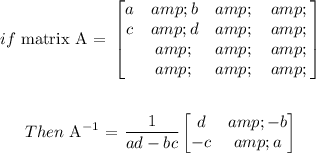
where in this case: a = -6 , b = 2 , c = 3 and d = -2

Substituting the values, we have it that:

`\begin{gathered} A^(-1)\text{ = }(1)/(-6(-2)-2(3))\text{ }\begin{bmatrix}{-2} & {-2} \\ {-3} & {-6}\end{bmatrix} \\ \\ A^(-1)\text{ = }(1)/(6)\begin{bmatrix}{-2} & {-2} \\ {-3} & {-6}\end{bmatrix} \end{gathered}`

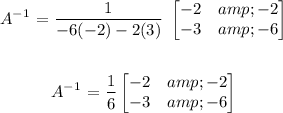
We proceed as follows:

Now, we multiply the inverse with the solution vector as follows:

`\begin{gathered} \begin{bmatrix}{x} & {} \\ {y} & {}\end{bmatrix}=\text{ }(1)/(6)\begin{bmatrix}{-2} & {-2} \\ {-3} & {-6}\text{ }\end{bmatrix}\begin{bmatrix}{-8} & {} \\ {-3} & {}\end{bmatrix} \\ \\ \end{gathered}`

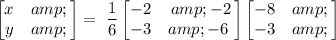
Finally, we have the product as:

`\begin{bmatrix}{x} & {} \\ {y} & {}\end{bmatrix}\text{ = }\begin{bmatrix}{(11)/(3)} & {} \\ {7} & {}\end{bmatrix}`