Step 1. Define our variables.
"x" will represent the ounces of the solution A
"y" will represent the ounces of the solution B.
Step 2. Define and equation for the total ounces of the solution mix.
Since we have to add the quantities x and y to get the solution, and we are told that the total of ounces is 50.
The sum of the ounces of solution A "x" and the sum of the ounces of solution B "y" must be equal to 50 ounces:
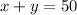
Step 3. Define a second equation for the percentage of salt.
solution A has 35% salt. Thus, in A, which has "x" ounces, we will have that 35% of x is salt:
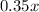
Note: we represent 35% as 0.35
Solution B has 60% of salt. Thus, in B, which has "y" ounces, we will have that 60% of y is salt:
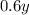
Note: we represent 60% as 0.6
Since the final mix (which has 50 ounces) has 45% of salt, the amount of salt is:
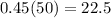
Note: we represent 45% as 0.45
We add the amount of salt in A 0.35x, and the amount of salt in B 0.6y to get the amount of salt in the mix:
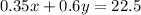
Step 4. Solve the system of equations.
The system of equation is:
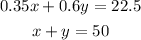
To solve this, we need to eliminate one variable.
Step 5. Multiply the second equation by (-0.35), the system now is:
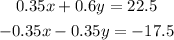
Note: the -17.5 is the result of -0.35x50
Step 6. Add the two equations to eliminate x:
Step 7. From the resulting equation of the last step, solve the equation for y:
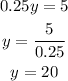
Step 8. Substitute this value of y into one of the original equations of the system, to find x.
We substitute y in the equation:
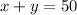
since y=20:
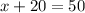
solving for x:
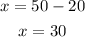
Answer:
how many ounces of each solution should she use?
since x=30, she should use 30 ounces of solution A.
And since y=20, she sould use 20 ounces of solution B.