The given inequality is
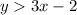
We have to evaluate each point in order to determine which one is a solution, and which one is not. Remember that the first number of a pair represents the value for x, and the second number represents the value for y.
(-7, 4).
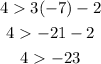
Notice that the result is true, 4 is more than -23. Hence, (-7, 4) is a solution.
(1, 0).
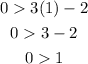
Zero is not more than 1, this result is false, which means (1,0) is not a solution.
(1, 6).
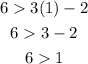
This result is true because 6 is greater than 1. Therefore, (1,6) is a solution.
(0, -2).
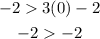
-2 is not greater than -2, they are equal, so (0, -2) is not a solution.
(4, -4).

-4 is not greater than 10, this result is false. Therefore, (4, -4) is not a solution.
In sum, the solutions are (-7, 4) and (1, 6).