Question

Students and adults purchased tickets for a recent school play. All tickets were sold atthe ticket booth (discounts of any type) were not allowed.Student tickets cost $8 each, and adult tickets cost $10 each. A total of $1,760 wascollected. 200 tickets were sold.C.Assuming that the number of students and adults attending would not change,how much more money could have been collected at the play if the student price waskept at $8 per ticket and adults were charged $15 per ticket instead of $10?

Answer 1

For this question we have to set up a system of equations.

Let

A= number of adult tickets

S= number of student tickets

then:

`\begin{gathered} A+S=200 \\ 8S+10A=1760 \end{gathered}`

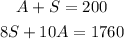
Solving the first equation for S ans susbtituting S in the second equation we get:

`\begin{gathered} S=200-A \\ 8(200-A)+10A=1760 \\ 1600-8A+10A=1760 \\ 2A=160 \\ A=80 \end{gathered}`

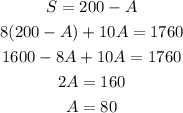
With the value of A we can get the value of S=200-A=200-80, S=120.

Finally if the adult ticket costs $15 instead of $10 and the student ticket remains the same, then the total earnings would be

`15A+8S=15(80)+8(120)=2160`

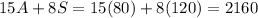
Answer: $2160.