Consider that the revenue is calculated as,

The current revenue of Mrs. Nicely is,
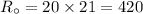
Let Mrs. Nicely lost 'x' students due to the fee hike. Now, there are (21-x) students remaining in her.
Given that every $4 increase in price results in loss of 1 student. The initial price was $20. So the price after 'x' students left will be (20+4x)$.
So the revenue function becomes,
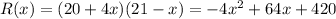
Now, obtain the stationary points as,
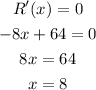
Apply the second derivative check,
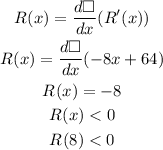
Since the second derivative is less than zero, the revenue function is maximum at x=8.
Thus, Mrs Nicely will have maximum revenue when 8 students have left, and the remaining students are (21-8=)13.
The corresponding price per student is calculated as,
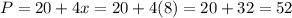
So Mrs. Nicely should charge $52 for tutoring in order to maximize her revenue.
And the maximum revenue is calculated as,
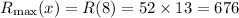
Thus, the maximum revenue she can expect is $676 each week.