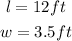Question

the area of a rectangle is 42ft squared and the length of the rectangle is 5 ft more then double the width. find the dimensions of the rectangle

Answer 1

The formula for calculate the area of a rectangle is:

`A=lw`

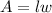
Where "l" is the length and "w" is the width,

According to the information given in the exercise:

`\begin{gathered} l=2w+5 \\ A=42 \end{gathered}`

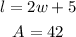
Then, you can set up the following equation:

`42=(2w+5)(w)`

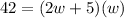
Simplify it:

`42=2w^2+5w`

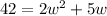
Make it equal to zero:

`2w^2+5w-42=0`

Use the Quadratic formula to find the value of "w":

`w=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this case:

`\begin{gathered} a=2 \\ b=5 \\ c=-42 \end{gathered}`

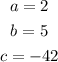
Substituting values and evaluating, you get:

`\begin{gathered} w=\frac{-5\pm\sqrt[]{5^2^{}-4(2)(-42)}}{2(2)} \\ \\ w_1=3.5 \\ w_2=-6 \end{gathered}`

Choose the positive value. Then:

`w=3.5ft`

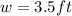
Substitute the width into the equation

`l=2w+5`

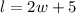
And then evaluate, in order to find the length of the rectangle. This is:

`\begin{gathered} l=2(3.5)+5 \\ l=12ft \end{gathered}`

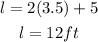
The answer is:

`\begin{gathered} l=12ft \\ w=3.5ft \end{gathered}`