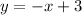Question

Find the equation of the tangent line to g(x) at x=5

Answer 1

We must find the equation of the tangent line for the function g(x) at the point x = 5, given:

`g(x)=\int ^x_0f(t)dt.`

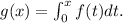
The general equation of the tangent line is:

`y=m\cdot x+b\text{.}`

where:

• m is the slope,

,

• b is the y-intercept.

1) Slope of the line

To find the equation of the line, first, we must find the slope of the line at x = 5, which is given by the derivative of the function g(x) at x = 5.

The Fundamental Theorem of Calculus says that:

`g^(\prime)(x)=(d)/(dx)\int ^x_0f(t)dt=f(x)\text{.}`

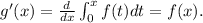
Using the graph of the function f, we get:

`g^(\prime)(5)=f(5)=-1.`

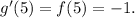
So the slope of the line tangent to g(x) at the point x = -1 is:

`m=g^(\prime)(5)=-1.`

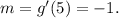
So the equation of the line has the form:

`y=h(x)=-x+b\text{.}`

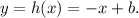
We must find the value of b.

2) y-intercept of the line

If the line is tangent to g(x) at the point with x = 5, the line must have the same value as g(x) at x = 5:

`y=h(5)=-5+b=g(5)\text{.}`

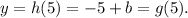
We must compute the value of g(5), which is given by:

`g(5)=\int ^5_0f(t)dt\text{.}`

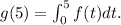
So the value of g(5) is the area under the curve f(t). Summing the different contributions, we get:

`g(5)=\int ^5_0f(t)dt=1+0.5-0.5-1.5-1.5=-2.`

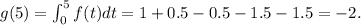
Replacing the result in the equation above, we get:

`\begin{gathered} -5+b=g(5), \\ -5+b=-2, \\ b=-2+5, \\ b=3. \end{gathered}`

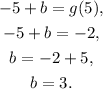
Using the value m = -1 and b = 3, the equation of the tangent line is:

`y=-x+3.`

Answer

`y=-x+3`