Question

I have no clue how to find the answer, I tried watching a video but it didn't have an explanation for a situation like this

Answer 1

Consider triangles ABC and ADE.

Notice that they share the same vertex A. Hence, they have congruent angle A.

Notice also that the measures of ∠ABC and ∠ADE are 90º, which implies that:

∠ABC ≅ ∠ADE.

Recall the Angle-Angle Similarity (AA~) Theorem which states that if two angles of one triangle and two angles of another triangle have the same measures, then the triangles are similar.

It follows that the triangles ABC and ADE are similar triangles:

`\triangle ABC\sim\triangle ADE`

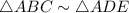
From the definition of similar triangles, their corresponding sides will be in proportion, that is:

`(AB)/(AD)=(BC)/(DE)`

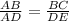
Substitute AB=2, AD=2+x, DE=2, and BC=1 into the equation:

`(2)/(2+x)=(1)/(2)`

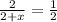
Solve the resulting equation for x:

`\begin{gathered} Cross\text{ multiply:} \\ 2+x=4 \\ \Rightarrow x=4-2=2 \end{gathered}`

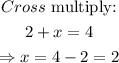
The answer is x=2.