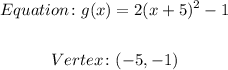Question

Write the quadratic function in the form g(x)=a (x-h)2 +kThen, give the vertex of its graph. G(x) =2x2 +20x+49Writing in the form specified: g(x) =Vertex =

Answer 1

The quadratic function given to us is:

`g(x)=2x^2+20x+49`

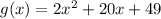
We are asked to find the vertex form of the function.

The general formula for the vertex form of a quadratic equation is:

`\begin{gathered} g(x)=a(x-h)^2+k \\ \text{where,} \\ (h,k)\text{ is the coordinate of the vertex} \end{gathered}`

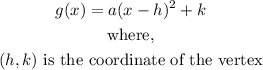
In order to write the function in its vertex form, we need to perform a couple of operations on the function.

1. Add and subtract the square of the half of the coefficient of x to the function.

2. Factor out the function with its repeated roots and re-write the equation.

Now, let us solve.

1. Add and subtract the square of the half of the coefficient of x to the function.

`\begin{gathered} g(x)=2x^2+20x+49=2(x^2+10x+(49)/(2)) \\ \text{half of coefficient of x:} \\ (10)/(2)=5 \\ \text{square of the half of the coefficient of x:} \\ 5^2=25 \\ \\ \therefore g(x)=2(x^2+10x+25-25+(49)/(2)) \end{gathered}`

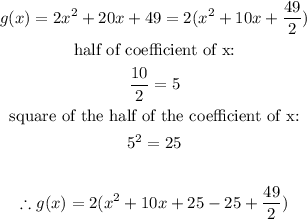
2. Factor out the function with its repeated roots and re-write the equation.

`\begin{gathered} g(x)=2(x^2+10x+25)-2(25+(49)/(2)) \\ re-\text{write the above function} \\ g(x)=2(x^2+10x+25)-1 \\ \text{Let us factorize this:} \\ g(x)=2(x+5)^2-1 \end{gathered}`

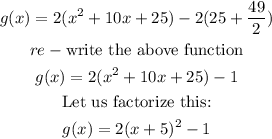
Therefore, we can conclude that the Equation and vertex of the equation is:

`\begin{gathered} Equation\colon g(x)=2(x+5)^2-1 \\ \\ Vertex\colon(-5,-1) \end{gathered}`