Question

6)Angles ZKLM and ZMLN are adjacent angles. Find the mZKLN, if mZKLM = 83° andmZMLN = 72º.

Answer 1

Here we will investigate the representation of "adjacent angles" and how to use this representation to solve for other angles.

Adjacent Angles: These angles are categorized by the following two properties.

`\begin{gathered} \text{Common adjacent side of two angles} \\ Common\text{ vertex of angles} \end{gathered}`

We are given that angles:

`\begin{gathered} \angle KLM\text{ \& }\angle\text{ MLN are adjacent angles} \\ \text{ } \end{gathered}`

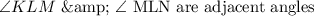
We will go ahead give a graphical representation of these adjacent angle so we have a better visualization:

We have expressed our two adjacent angles KLM and MLN. Where,

`\begin{gathered} LM\text{ = Common Adjacent side} \\ L\text{ = Common vertex} \end{gathered}`

The respective included angles are given as follows:

`\begin{gathered} m\angle KLM=83^o \\ m\angle MLN=72^o \end{gathered}`

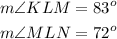
We are asked to find the complete interior angle:

`m\angle KLN`

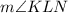
Since all the given angles lie in the same plane of paper these angles are considered to be one-dimensional angles. We can express the required angle m

We will go ahead and express the above one-dimensional composite angle mathematically:

`\textcolor{#FF7968}{m\angle KLN}\text{\textcolor{#FF7968}{ = m}}\textcolor{#FF7968}{\angle KLM}\text{\textcolor{#FF7968}{ + m}}\textcolor{#FF7968}{\angle MLN}`

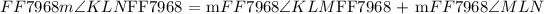
A composite angle eliminates the adjacent side ( LM or ML ) but retains the common vertex ( L ) and comprised of the outermost sides of the two adjacent angles ( KL and LN ).

We will go ahead and use the expression developed to determine the required angle:

`\begin{gathered} m\angle KLN=83^o+72^o \\ \textcolor{#FF7968}{m\angle KLN=155^o} \end{gathered}`

For the next question we are given the angles:

`\text{Anlges }\angle\text{PQO \& }\angle PQR\text{ are adjacent angles}`

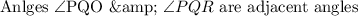
We will go ahead give a graphical representation of these adjacent angle so we have a better visualization:

We have expressed our two adjacent angles PQO and PQR. Where,

`\begin{gathered} PQ\text{ = Common Adjacent side} \\ Q\text{ = Common vertex} \end{gathered}`

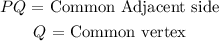
The respective included angles are given as follows:

`\begin{gathered} m\angle OQR=170^o\text{ } \\ m\angle PQR=84^o \end{gathered}`

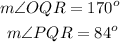
We are asked to find the constitutent angle of a composite angle:

`m\angle PQO`

Since all the given angles lie in the same plane of paper these angles are considered to be one-dimensional angles. We can express the angle m

We will go ahead and express the above one-dimensional composite angle mathematically:

`\textcolor{#FF7968}{m\angle OQR}\text{\textcolor{#FF7968}{ = m}}\textcolor{#FF7968}{\angle PQO}\text{\textcolor{#FF7968}{ + m}}\textcolor{#FF7968}{\angle PQR}`

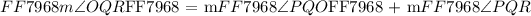
A composite angle eliminates the adjacent side ( PQ ) but retains the common vertex ( Q ) and comprised of the outermost sides of the two adjacent angles ( OQ and QR ).

We will go ahead and use the expression developed to determine the required angle:

`\begin{gathered} 170^o\text{ = m}\angle PQO+84^o \\ \text{m}\angle PQO=170^o-84^o \\ \textcolor{#FF7968}{m\angle PQO=86^o} \end{gathered}`